Музыка и гармония Вселенной

(о работах Л. Эйлера и И. Кеплера, связанных

с теорией музыки и открытием 390 лет назад

«основного уравнения астрономии»)

В фундаментальных трудах И. Кеплера, относящихся к 1610–1619 гг., и Л. Эйлера – 1739 г. разработаны законы теории музыки, выступающие в качестве «метода гармонии» для познания и обоснования основополагающих математических и физических (включая третий закон Кеплера) закономерностей. Выступая как «композитор-астроном», Кеплер строит контрапункт планет. Введение Кеплером понятия формообразующей силы дает возможность на основе механизма золотого или, по Кеплеру, «божественного» сечения формулировать законы развития в природе, имеющие антиэнтропийный характер. «Метод гармонии» позволяет объяснить действие кеплеровской «формообразующей» силы, объясняет закономерности развития во времени физических процессов, до сих пор не нашедших должной формулировки при изложении курса физики.

Гармония мира, проявляющаяся в виде особой формы симметрии, нашла частное отражение в музыке, особенно классической. В виде обратной связи для многих выдающихся ученых (Л. Эйлер, И. Кеплер и другие) музыка послужила методом познания и открытия универсальных мировых законов физики и математики. Так, у Гельмгольца^[1] читаем следующее: «Как часто долго можно сидеть на берегу и смотреть на движущиеся волны! Их ритмическое движение производит чувство благотворения, успокоения и дает впечатление могущественной и прекрасно составленной жизни. Движение воды (будь оно в водопадах или морских волнах) аналогично музыкальному впечатлению».

Великий ученый XVIII в. Леонард Эйлер (1707–1783 гг.), член Петербургской академии наук, среди более 850 своих научных трудов ряд работ посвятил музыке. Одна из первых больших работ Л. Эйлера – «Dissertatio physico de sono» – посвящена природе, образованию и распространению звука. В 1726 г. Л. Эйлер писал Даниилу Бернулли^[2], что для ноты «до» он в результате исследования получил 139 колебаний в секунду. В 1727 г. Л. Эйлер, находясь в Петербурге, составляет отчет о своей работе в виде «исчисления всех дел, елико ко умножению и совершенству наук принадлежат, доселе произвели и что впредь произвести намерены…

Л. Эйлер, профессор высшей математики адъюнкт, уже исследованию предложил:

1. Физико-математическое рассуждение о звуке или звоне, в котором новая звону теория предается и поставляется, откуда производится образ счисления (вычисления. – В. С.) скорости звука;
2. Рассуждение о качательном (колебательном. – В. С.) движении струн, колоколов, барабанов, которые через ударение звон издают, где от теории каждого инструмента изъявляется образ счисления скорости звука;
3. О произведении звона или звука пушечного, громового и прочих таковых.
4. Новая теория о звонах или голосах флейт, труб идругих инструментов, которые через надувание глас издают».

Основным трудом Л. Эйлера по вопросам теории музыки стала «Tentamen novae theoriae musicae, ex certissimis harmoniae principiis dilucide expositae»^[3], напечатанная в 1739 г. в Санкт-Петербурге и найденная автором в научной библиотеке Одесского госуниверситета. Музыку Л. Эйлер воспринимал как гармонию пропорций. Возможно, такие представления были заимствованы у И. Кеплера из его капитального труда «Welt-Harmonik» («Гармония мира»), изданного в 1619 г. во Франкфурте и переизданного в Мюнхене – Берлине в 1939 г. («Земля и Вселенная», 2002, № 5).

Как писал в своем труде Л. Эйлер, его теория музыки строится на двух основаниях: физическом (физические законы звука) и метафизическом (изучение восприятия звука). Л. Эйлер рассматривает вопрос: что есть общего между консонансами и отношениями целых чисел, соответствующих, согласно современной терминологии, частотам колебаний струн, образующих созвук при одновременном звучании, вызванном этими струнами? Ответ на подобный вопрос частично дали И. Кеплер и даже древний философ Пифагор.

Со времен Пифагора известна легенда о том, что Пифагор, проходя мимо кузницы, услышал звуки, которые издавали два молота, стучавшие по наковальне. Получилось соотношение музыкальных тонов, дававших определенный музыкальный интервал. Пифагор сравнил молоты и нашел, что по их форме и размерам можно было найти такое же отношение (пропорцию) при звучании, вызванном колебаниями струн. Оказалось, что чистая кварта дает отношение 4:3, квинта – 3:2, секста – 5:3, большая терция – 5:4, малая терция – 6:5. Следовательно, отношение простых чисел дает восприятие консонанса, а секунда (16:15) воспринимается как диссонанс. Л. Эйлер пишет: «Если мы при восприятии звуков не улавливаем никакого порядка или этот порядок неожиданно нарушается, мы не можем почувствовать удовлетворения». Иначе говоря, слушателю приятно все то, в чем он улавливает завершенность, определенный порядок. Такой порядок создается при наличии определенного правила, из которого можно сделать заключение, почему часть целого помещена в том или ином месте. Такое рассуждение напоминает о понятии, создающем образ гармонии при делении отрезка в средне-пропорциональном отношении, когда, в частности, целое так относится к большей своей части, как большая часть – к меньшей:

при а = 1, b = x, x² – x – 1 = 0.

Так эта пропорция превращается в уравнение с корнями ± Ф, обладающими рядом удивительных свойств.
Например, если число n = 0, 1, 2, 3…∞, то корни приведенного уравнения могут составить следующую зависимость: Фⁿ + Фⁿ⁺¹ = Фⁿ⁺², которая определяет единство аддитивных и мультипликативных свойств этих чисел, образующих ряды Фибоначчи, благоприятно осуществляемые при развитии всевозможных природных явлений (например, размножение кроликов)^[4]. О записанной выше «божественной пропорции», или «божественном» (золотом) сечении, уже сказал И. Кеплер при рассмотрении геометрии снежинок.

Как выяснилось в дальнейшем, осуществление золотого сечения в природе определяет в огромном числе случаев не только музыкальное восприятие, но и само развитие этой природной формы в наиболее благоприятном направлении, например развитие листьев или рост кроны дерева. В книге «О шестиугольных снежинках» (в переводе с латинского эта книга выпущена на русском языке издательством «Наука» в Москве в 1982 г. по изданию 1611 г. во Франкфурте-на-Майне) Кеплер писал: «По образцу и подобию продолжающей саму себя пропорции сотворяется, как я полагаю, производительная сила, и этой производительной силой запечатлен в цветке смысл пятиугольника».

В специальном сборнике докладов, сделанных на 6-м съезде Европейского и национальных астрономических обществ Jenam-97, проходившем 2–5 июля 1997 г. в Салониках (Греция), в разделе «История астрономии» отмечен вывод автора статьи о том, что «метод гармонии И. Кеплера объясняет существование антиэнтропийных процессов, широко распространенных в природе». Другими словами, этот метод позволяет объяснить действие кеплеровской «формообразующей» силы, объясняет закономерности развития во времени физических процессов, до сих пор не нашедших должной формулировки при изложении курса физики.

В третьей части книги «Гармония мира» Кеплер изложил свою теорию разрешения музыкальных интервалов: «мелодия, поднявшись от основного тона, должна вернуться к нему». Кеплер приводит рассуждение о том, что составляет природу благозвучия при пении, замечая, что в трубных звуках инструментов турок и венгров «содержится подражание диким животным». Ученый критикует употребление запрещенных интервалов при пении, так как такая музыка «не может быть удержана в памяти слушателя, бессвязна и недопустима». Мелодия должна быть благозвучной, «соответствовать суждению слуха, должна исходить из определенного основного тона через интервалы и возвращаться к нему».

«Диссонирующие интервалы, – пишет И. Кеплер, – должны пробегать быстро, но консонирующие должны задерживаться». Кеплер на основе своей теории вводит рекомендации для употребления интервалов при композиции. Перечислим некоторые из этих рекомендаций И. Кеплера:

– диез не дает мелодии перед полутоном;

– два полутона допустимы, если они следуют друг за другом в последовательности малых интервалов;

– два полутона внутри кварты не мелодичны;

– не мелодичны четыре целых тона, следующие друг за другом;

– не мелодична септима и другие интервалы через октаву;

– сексты допускаются изредка. Консонируют малые сексты;

– не рекомендуется использовать два тетрахорда одной октавы;

– запрещено использование трех целых тонов, следующих друг за другом;

– два полутона также немелодичны;

– октавные системы немелодичны, если внизу не лежит кварта или квинта. Как и Эйлер, Кеплер настоятельно советует избегать диссонирующих интервалов.

И. Кеплер применил октавный принцип при сравнении угловых скоростей планет в перигелии и афелии и получил «основное уравнение астрономии», которое в учебниках записывается как равенство отношений квадратов периодов обращений планет вокруг Солнца и кубов их средних расстояний до Солнца. При этом он пользовался таблицами, определяющими эфемериды планет, составленными его предшественником Тихо Браге – астрономом императора Рудольфа в Праге, которого Кеплер не без основания называл своим благодетелем. В формулировке Кеплера третий закон в русском переводе выглядит так: «Пропорция между периодами обращения любых двух планет составляет ровно полторы пропорции их средних расстояний». Попутно с получением «основного уравнения астрономии», по которому ведутся расчеты небесной механики, вычисления эфемерид планет на многие годы вперед, Кеплер находит зависимость между расстояниями планет от Солнца в афелии и перигелии и их наибольшей и наименьшей угловой скоростью на орбите.
Отношения скоростей составляли гармонические интервалы, в большинстве случаев – «консонансы». Таким отношениям угловых скоростей в афелии и перигелии на орбите Сатурна можно было сопоставить большую терцию (4:5), на орбите Юпитера – малую терцию (5:6), на орбите Марса – квинту (2:3), но на орбите Земли – диссонирующий полутон (15:16), на орбите Венеры – диезис (24:25), на орбите Меркурия – октаву с малой терцией (5:12).

При построении звукоряда Кеплер отдал предпочтение натуральной, «доказанной» системе звуков, используя следующие символы: до (ут), ре, ми, фа, соль, ля. Кеплер подробно изучил возможности построения октавной системы. Отсутствие седьмой ноты в системе, образующей септиму, можно связать с желанием соединить число известных в то время планет с числом нот в октаве, хотя в книге об этом ничего не сказано. При построении октавных систем Кеплер ссылается на работу Винченцо Галилея (отца Галилео Галилея) «Диалог об античной и новой музыке», изданной в 1581 г. во Флоренции. В одном из писем Кеплер сообщил, что впервые прочитал эту работу по дороге в Линц, куда ехал к своей матери, обвиненной в колдовстве. Октаву Кеплер строит на тринадцати струнах с помощью следующих мелодических интервалов: полутон, лимма, полутон, диезис, полутон, полутон, лимма, полутон, диезис, полутон, полутон, лимма. Вообще современный звукоряд образуется следующим образом: если октавный промежуток, соответствующий пропорции между числами колебаний струн 1:2, разделить на 12 равных частей (по ступеням гаммы), то получается «хорошо темперированный строй», используемый преимущественно в современной музыке. Числа, отражающие пропорции частот колебаний между ступенями гаммы, выразятся в виде ряда:

2⁰ 2^1/12 2^2/12 2^3/12 2^4/12 2^5/12 2^6/12 2^7/12 2^8/12 2^9/12 2^10/12 2^11/12 2^12/12.

Полученные геометрические и небесно-механические соотношения Кеплер анализирует, чтобы выявить число октав в различных числовых промежутках. Например, согласно сделанному расчету, между угловыми суточными движениями Земли и Сатурна в афелии содержится пять октав.

Для вычисления музыкальных пропорций Л. Эйлер ввел логарифмы при основании 2, поскольку для октавы (логарифм отношения 2:1) такие логарифмы дают целое число – единицу. Тогда при каком-либо переходе на октаву десятичная дробь после запятой остается без изменения и требует лишь прибавления или вычитания единицы. Эти данные при развитии теории музыки неоднократно использовались в дальнейшем. Например, в «Музыкальном словаре» Г. Римана логарифмы Эйлера использованы для математического определения соотношения тонов по высоте. Для описания благозвучия интервалов Эйлер вводит степени благозвучия – gradus suanitatis, о которых говорил еще Кеплер. Эти численные определения благозвучия интервалов и аккордов Эйлер находит по следующему арифметическому правилу (отметим, что такой математический подход вполне обоснован для различных применений, поскольку математические символы при разных физических применениях остаются неизменными). По Эйлеру, для простых натуральных чисел степень благозвучия совпадает со значением такого числа. Все остальные числа рассматриваются как произведения упомянутых «начальных» чисел. Степень благозвучия произведения простых чисел равна сумме этих чисел минус единица. Если находится степень благозвучия аккорда, то находится наименьшее число, которое делилось бы на все наименьшие множители в соотношении чисел колебаний. Например, для четырех степень благозвучия определяется так: 2 + 2 – 1 = 3.
Для двенадцати (4:3) степень благозвучия четырех равна 3, откуда получаем степень благозвучия для 12 : 3 + 3 – 1 = 5. Для натуральной септимы (4:7) наименьшее число, которое делится на 4 и 7, есть 28 = 4∙7. Но степень благозвучия четырех есть 3, тогда степень благозвучия для септимы будет: 3 + 7 – 1 = 9. Эйлер писал, что найденные таким образом степени благозвучия являются важным элементом в музыке и в других областях искусства. Эйлер, как и Кеплер, изучал не только отдельные консонансы и аккорды, но и их последовательности, занимался построением гамм и модуляций. Одна из систем тонов, выведенная Эйлером, почти полностью совпадает с диатонично-хроматической, которую используют в настоящее время музыканты.

Для И. Кеплера сопоставление различных музыкальных пропорций, известных еще древним, не просто предмет исследования, а серьезный метод, инструмент, которым он пользуется для изучения закономерностей движения небесных светил. Для построения и определения орбит планетной системы Кеплер использовал правильные вписанные и описанные многогранники (платоновы фигуры). Применение подобной методики к вибрирующей струне позволило выявить в колебаниях ее частей музыкальные интервалы, а также звучания, которые впоследствии позволили определить тембр звука – обертоны. Найденные Кеплером пропорции между консонирующими интервалами одновременно определяли количественные соотношения между используемыми платоновыми фигурами.

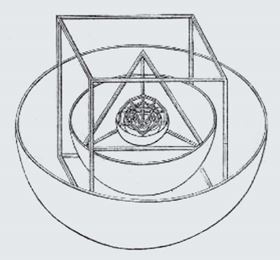
Кеплер показывает структуру планетных орбит на основе построения платоновых вписанных и описанных фигур. Так, если вокруг орбиты Земли, которая является общей мерой всех других орбит, описать додекаэдр, а вокруг додекаэдра – сферу, получим орбиту Марса, соответствующую такой сфере. Если вокруг орбиты Марса, связанной с описанной сферой, описать тетраэдр, а вокруг тетраэдра – сферу, получится сфера орбиты Юпитера. Если вокруг орбиты Юпитера описать куб, а вокруг куба – сферу, получим сферу орбиты Сатурна. Вписанные в сферу орбиты Земли икосаэдр и сфера дают сферу орбиты Венеры. Наконец, если вписать в сферу орбиты Венеры октаэдр и в него вписать сферу, то получим орбиту Меркурия. В ряде статей автор объясняет получаемые таким образом построения орбит известных во времена Кеплера планет, а также правило Тициуса – Боде наличием общей меры в виде длины энергетической стоячей волны, хотя данные понятия
не были известны во времена Кеплера и Эйлера. Планетные расстояния в этом случае легко определяются из уравнения стоячей волны.

Согласно нашим расчетам в узловых точках стоячих волн, действовавших при образовании Солнечной системы в первичном газопылевом облаке, как и в наглядном случае эксперимента по образованию фигур Хладни, должны были образовываться сгущения вещества в виде протопланет и протоспутников. Введя длину стоячей волны λ, можно, используя формулу волны, образованную гармоническими колебаниями источника волны, определяемого орбитой Меркурия, измерять расстояния планет от Солнца либо спутников от планет. При этом также выявляются закономерности золотого сечения.

Итак, золотое сечение вместе со связанным с ним рядом чисел является формообразующей субстанцией, облегчающей развитие в выбранном направлении различных природных явлений, в данном случае – Солнечной системы. При такой трактовке остается ряд неопределенностей, связанных с отсутствием формулировок физических законов развития, носящих антиэнтропийный характер. К сожалению, при изложении законов физики всегда подчеркиваются формулировки стационарных законов сохранения, но не указывается на известный факт наличия законов изменения во времени физических величин. Например, приведем формулу механической работы:

ΔА = FΔs соs (F, Δs),

где F – действующая сила, Δs – перемещение тела, совершающего работу, при которой соответственно изменяется его энергия, эквивалентная совершению работы. В этой формуле для ΔА показаны процессы, совершающиеся во времени Δt, то есть это – закон изменения энергии. Однако обычно при изложении законов физики формулируются одномерные стационарные случаи, вытекающие из постоянства физических величин во времени, описывающие состояния изолированных систем. Упомянутые антиэнтропийные законы развития, связанные, по Кеплеру, с действием формообразующей силы, показывают направленность процесса развития, но пока четко не сформулированы.

В связи с этим интересно подумать и о развитии в целом музыкальной культуры, учитывая, по Кеплеру, действие «божественного» (золотого) сечения. Конечно, при качественном изучении данной проблемы развитие музыкальной культуры вписывается в пропорции золотого сечения, теорию консонансов. Между тем в последние десятилетия музыкальная культура развивалась под большим воздействием английского языка, хотя, ставший мировым, он сам по себе не обладает какой-либо особой музыкальностью. Доказательством этого, пишет в своих дневниках В. А. Швец^[5], является то обстоятельство, что англоязычные народы не дали ни одного композитора, стоявшего на уровне Бетховена, Верди, Скрябина, Чайковского или Шуберта. Представители массовой культуры чаще всего создают в своих произведениях диссонирующие шумовые эффекты, отражающие звуки исчезающих с поверхности Земли джунглей. Такое развитие вносит противоречие в закономерности, вытекающие из золотого сечения, и говорит о том, что английский язык cтал мировым лишь по политическим причинам.

^[1] Гельмгольц Герман Людвиг Фердинанд (1821–1894).

^[2] Бернулли Даниил (1700–1782).

^[3] На русском языке название книги Л. Эйлера выглядит так: «Опыт новой теории музыки, ясно изложенный на основе несомненных принципов гармонии». Перевод книги в 1959 г. автору статьи помогала осуществлять преподаватель ОГУ Н. Л. Сикорская, которой автор остается благодарен и поныне. Методическую помощь при написании студенческой работы, за которую автор получил премию, оказывали преподаватель школы Столярского В. А. Швец и доцент кафедры математического анализа университета С. Н. Киро, которым автор также выражал благодарность, но напечатать в студенческой работе это не разрешили. Поэтому уместно эту благодарность выразить в данное время, через 50 лет после написания работы.

^[4] В математике аддитивность означает, что каждый предыдущий член ряда чисел Ф₁, Ф₂, Ф₃… равен сумме двух последующих: Ф₁ = Ф₂ + Ф₃ и т. д. Мультипликативность означает, что в том же числовом ряду все члены связаны геометрической прогрессией: Ф₁:Ф₂ = Ф₂:Ф₃.

^[5]  См. серию книг «Реквием ХХ века» В. А. Смирнова. Одесса, 2001–2007 гг.

Об авторе:

Родился 5 апреля 1936 года в Одессе, преподаватель физики, советский, российский и украинский астроном, историк науки и писатель. В течение 7 лет секретарь партбюро факультета автоматической электросвязи ОЭИС им А. С. Попова, в течение 17 лет председатель правления ЖСК «Ленинский-26». В течение 10 лет исполнял обязанности ответственного секретаря Всесоюзного астрономо-геодезического общества (ВАГО), а также был членом ученого совета ОГУ им. И. И. Мечникова. Автор законченной серии книг «Реквием XX века», объемом около 6000 страниц текста, а также единственной по данной тематике монографии «Спектры кратковременных атмосферных световых явлений: метеоры». Автор более 100 статей в научных изданиях и СМИ, кандидат физико-математических наук, доцент кафедры физики.

Опубликовано в альманахе «Российский колокол» № 2-2021.
Размещено на сайте 23.08.2021 в 20:47.